Research

My interests lie at the intersection of exoplanet science, instrumentation and computational imaging. Here are a few current and previous projects that I have worked on.

Differentiable coronagraph modelling for starlight subtraction

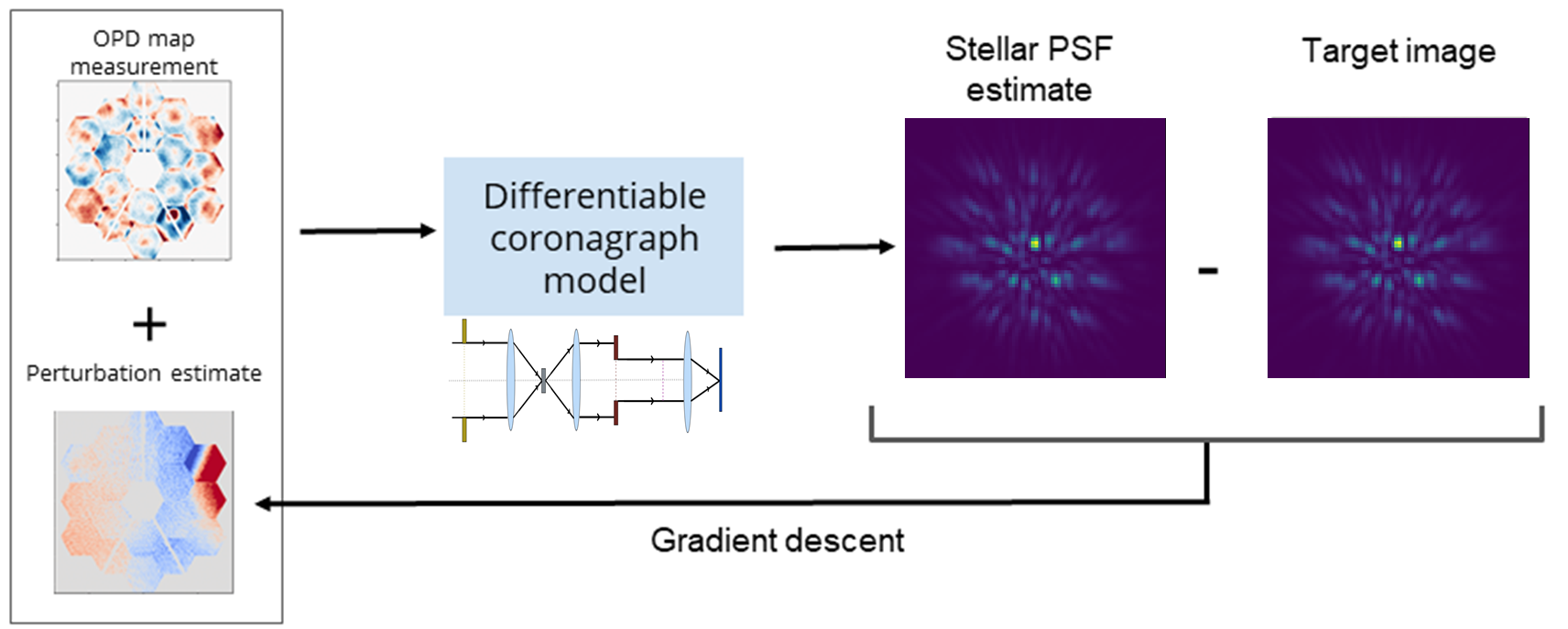
A major challenge in exoplanet imaging is to effectively remove starlight from our observations while keeping the light from the planet. Due to planets being orders-of-magnitude fainter than their host star, even small residuals of starlight can hide a planet. Current methods to remove starlight consist on taking reference images and using Principal Component Analysis (PCA) to model our star of interest, so that we can remove that starlight model from our images.

In collaboration with Brandon Y. Feng, Prof. Katie Bouman and Prof. Aviad Levis, we are developing a forward-modelling alternative approach for starlight subtraction. See here for our paper.

Biases in orbit-fitting of directly-imaged exoplanets

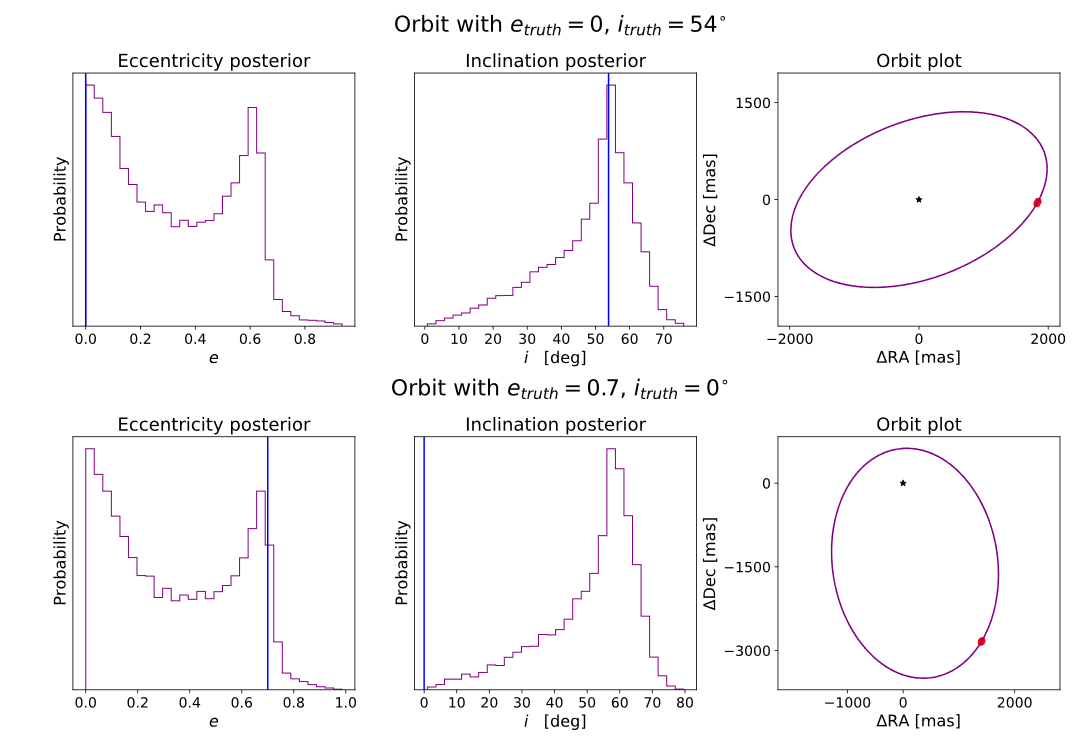
Direct-imaging is most sensitive to planets very far from their star, where they are easier to detect. Given that the orbital period of a planet increases as its semi-major axis increases (by Kepler's third law), directly-imaged planets tend to have relatively long periods, some even up to hundreds or thousands of years. This means that even with years of observations, we often times can see the planet only moving through a small fraction of its orbit, making the inference of the orbit of the planet very challenging.

Given that reliably fitting the orbit of a planet can reveal vital information about its formation, history and environment, in collaboration with Jason Wang and Sarah Blunt I carried out a systematic statistical analysis of the biases we are most prone to when estimating orbits of directly-imaged planets. Performing our analyses with widely-used Bayesian frameworks and setups, we characterize biases such as the eccentricity-inclination degeneracy and the coverage of the credible intervals over orbital parameters. See here for our paper.